Kalor jenis
Rumus:
dengan ketentuan:
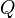 = Kalor yang diterima suatu zat (Joule, Kilojoule, Kalori, Kilokalori)
= Kalor yang diterima suatu zat (Joule, Kilojoule, Kalori, Kilokalori) = Massa zat (Gram, Kilogram)
= Massa zat (Gram, Kilogram) = Kalor jenis (Joule/kilogram°C, Joule/gram°C, Kalori/gram°C)
= Kalor jenis (Joule/kilogram°C, Joule/gram°C, Kalori/gram°C) = Perubahan suhu (°C) → (t2 - t1)
= Perubahan suhu (°C) → (t2 - t1)

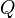 = Kalor yang diterima suatu zat (Joule, Kilojoule, Kalori, Kilokalori)
= Kalor yang diterima suatu zat (Joule, Kilojoule, Kalori, Kilokalori) = Massa zat (Gram, Kilogram)
= Massa zat (Gram, Kilogram) = Kalor jenis (Joule/kilogram°C, Joule/gram°C, Kalori/gram°C)
= Kalor jenis (Joule/kilogram°C, Joule/gram°C, Kalori/gram°C) = Perubahan suhu (°C) → (t2 - t1)
= Perubahan suhu (°C) → (t2 - t1)
 Hukum dasar mekanika terbukti mampu menjelaskan berbagai fenomena yang berhubungan dengan sistem diskrit (partikel). Hukum dasar ini tercakup dalam formulasi Hukum Newton tentang gerak. Selain sistem diskrit di alam ini terdapat bentuk sistem lain yaitu sistem kontinyu yang mencakup benda tegar dan fluida. Pada bagian ini akan dibahas formulasi hukum mekanika pada benda tegar yang pada akhirnya akan diperoleh bahwa hukum-hukum yang berlaku pada sistem diskrit juga berlaku pada sistem kontinu ini.
Hukum dasar mekanika terbukti mampu menjelaskan berbagai fenomena yang berhubungan dengan sistem diskrit (partikel). Hukum dasar ini tercakup dalam formulasi Hukum Newton tentang gerak. Selain sistem diskrit di alam ini terdapat bentuk sistem lain yaitu sistem kontinyu yang mencakup benda tegar dan fluida. Pada bagian ini akan dibahas formulasi hukum mekanika pada benda tegar yang pada akhirnya akan diperoleh bahwa hukum-hukum yang berlaku pada sistem diskrit juga berlaku pada sistem kontinu ini.Hukum ini juga disebut hukum inersia atau prinsip Galileo
''Jika resultan gaya pada suatu benda sama dengan nol, maka benda yang mula-mula diam akan terus diam. Sedangkan, benda yang mula-mula bergerak, akan terus bergerak dengan kecepatan tetap''
Hukum Newton I dapat diinterpretasikan sebagai berikut :
Pernyataan tersebut dapat dinyatakan dengan 
Keterangan :
Pernyataan tersbut, dalam notasi kalkulus, dapat dinyatakan dengan 
Keterangan :
 adalah diferensial kecapatan terhadap waktu
adalah diferensial kecapatan terhadap waktuHukum Newton I menjelaskan kerangka acuan di mana hukum II dan hukum III Newton dapat dibuktikan benar. Kerangka acuan ini disebut kerangka acuan inersial atau kerangka acuan Galilean.
Perkembangan hukum ini dapat ditelusuri hingga Aristoteles. Aristoteles membagi gerak menjadi dua, yaitu gerak alami dan gerak paksa, dalam hal gerak alami, menurutnya setiap benda akan mencari keadaan alaminya (eg. benda berat jatuh kebawah, benda ringan terbang keatas) dan menyatakan bahwa gerak melingkar adalah gerak alami yang tidak disebabkan oleh gaya. Dalam hal gerak paksa, Aristoteles berpendapat bahwa gerak paksa disebabkan oleh gaya luar yang bekerja pada suatu benda dan jika pada suatu benda tidak bekerja gaya luar, maka benda tersebut akan kembali ke keadaan alaminya yaitu diam.
Setelah Aristoteles, Galileo melakukan percobaan sendiri mengenai gerak dengan menggunakan bola dan menyimpulkan bahwa bola yang bergerak akan diperlambat kelajuannya sampai berhenti oleh gaya gesek. Pengamatan dan kesimpulan Galileo kemudian dipelajari dan dikembangkan oleh Newton untuk menyusun hukum pertamanya.
Jika suatu gaya total bekerja pada benda, maka benda akan mengalami percepatan, di mana arah percepatan sama dengan arah gaya total yang bekerja padanya. Vektor gaya total sama dengan massa benda dikalikan dengan percepatan benda.

m adalah massa benda dan a adalah (vektor) percepatannya. Jika persamaan di atas ditulis dalam bentuk a = F/m, tampak bahwa percepatan sebuah benda berbanding lurus dengan resultan gaya yang bekerja padanya dan arahnya sejajar dengan gaya tersebut. Tampak juga bahwa percepatan berbanding terbalik dengan massa benda.

Jadi apabila tidak ada gaya total alias resultan gaya yang bekerja pada benda maka benda akan diam apabila benda tersebut sedang diam; atau benda tersebut bergerak dengan kecepatan tetap, jika benda sedang bergerak. Ini merupakan bunyi Hukum I Newton.
Setiap gaya F merupakan vektor yang memiliki besar dan arah. Persamaan hukum II Newton di atas dapat ditulis dalam bentuk komponen pada koordinat xyz alias koordinat tiga dimensi, antara lain :

Satuan massa adalah kilogram, satuan percepatan adalah kilogram meter per sekon kuadrat (kg m/s2). Satuan Gaya dalam Sistem Internasional adalah kg m/s2. Nama lain satuan ini adalah Newton; diberikan untuk menghargai jasa eyang Isaac Newton. Satuan-satuan tersebut merupaka satuan Sistem Internasional (SI). Dengan kata lain, satu Newton adalah gaya total yang diperlukan untuk memberikan percepatan sebesar 1 m/s2 kepada massa 1 kg. Hal ini berarti 1 Newton = 1 kg m/s2.
Dalam satuan CGS (centimeter, gram, sekon), satuan massa adalah gram (g), gaya adalah dyne. Satu dyne didefinisikan sebagai gaya total yang diperlukan untuk memberi percepatan sebesar 1 cm/s2 untuk benda bermassa 1 gram. Jadi 1 dyne = 1 gr cm/s2.
Kedua jenis satuan yang kita bahas di atas adalah satuan Sistem Internasional (SI). Untuk satuan Sistem Inggris (British Sistem), satuan gaya adalah pound (lb). 1 lb = 4,45 N. Satuan massa = slug. Dengan demikian, 1 pound didefinisikan sebagai gaya total yang diperlukan untuk memberi percepatan sebesar 1 ft/s2 kepada benda bermassa 1 slug.
Dalam perhitungan, sebaiknya anda menggunakan satuan MKS (meter, kilogram, sekon) SI. Jadi jika diketahui satuan dalam CGS atau sistem British, terlebih dahulu anda konversi.
HUKUM III NEWTON
Apabila sebuah benda memberikan gaya kepada benda lain, maka benda kedua memberikan gaya kepada benda yang pertama. Kedua gaya tersebut memiliki besar yang sama tetapi berlawanan arah.
Secara matematis Hukum III Newton dapat ditulis sebagai berikut :
F A ke B = – F B ke A
F A ke B adalah gaya yang diberikan oleh benda A kepada benda B, sedangkan F B ke A adalah gaya yang yang diberikan benda B kepada benda A. Misalnya ketika anda menendang sebuah batu, maka gaya yang anda berikan adalah F A ke B, dan gaya ini bekerja pada batu. Gaya yang diberikan oleh batu kepada kaki anda adalah – F B ke A. Tanda negatif menunjukkan bahwa arah gaya reaksi tersebut berlawanan dengan gaya aksi yang anda berikan. Jika anda menggambar tanda panah yang melambangkan interaksi kedua gaya ini, maka gaya F A ke B digambar pada batu, sedangkan gaya yang diberikan batu kepada kaki anda, – F B ke A, digambarkan pada kaki anda.
Persamaan Hukum III Newton di atas juga bisa kita tulis sebagai berikut :
Faksi = -Freaksi
Hukum warisan eyang Newton ini dikenal dengan julukan hukum aksi-reaksi. Ada aksi maka ada reaksi, yang besarnya sama dan berlawanan arah. Kadang-kadang kedua gaya tersebut disebut pasangan aksi-reaksi. Ingat bahwa kedua gaya tersebut (gaya aksi-gaya reaksi) bekerja pada benda yang berbeda. Berbeda dengan Hukum I Newton dan Hukum II Newton yang menjelaskan gaya yang bekerja pada benda yang sama.
Gaya aksi dan reaksi adalah gaya kontak yang terjadi ketika kedua benda bersentuhan. Walaupun demikian, Hukum III Newton juga berlaku untuk gaya tak sentuh, seperti gaya gravitasi yang menarik buah mangga kesayangan anda. Ketika kita menjatuhkan batu, misalnya, antara bumi dan batu saling dipercepat satu dengan lain. batu bergerak menuju ke permukaan bumi, bumi juga bergerak menuju batu. Gaya total yang bekerja pada bumi dan batu besarnya sama. Bumi bergerak ke arah batu yang jatuh ? masa sich… karena massa bumi sangat besar maka percepatan yang dialami bumi sangat kecil (Ingat hubungan antara massa dan percepatan pada persamaan hukum II Newton). Walaupun secara makroskopis tidak tampak, tetapi bumi juga bergerak menuju batu atau benda yang jatuh akibat gravitasi. Bumi menarik batu, batu juga membalas gaya tarik bumi, di mana besar gaya tersebut sama namun arahnya berlawanan.
Hukum III Newton dalam Kehidupan Sehari-hari
Konsep Hukum III Newton sebenarnya sering kita alami dalam kehidupan sehari-hari, walau kadang tidak kita sadari. Hal apa saja dalam kehidupan sehari-hari yang menggunakan konsep Hukum III Newton ?
Hukum III Newton berlaku ketika kita berjalan atau berlari
Ketika berjalan, telapak kaki kita memberikan gaya aksi dengan mendorong permukaan tanah atau lantai ke belakang. Permukaan tanah atau lantai memberikan gaya reaksi kepada kita dengan mendorong telapak kaki kita ke depan, sehingga kita berjalan ke depan. Ketika berjalan mundur, telapak kaki kita mendorong permukaan tanah atau lantai ke depan. Sebagai reaksi, permukaan tanah atau lantai mendorong telapak kaki kita ke belakang sehingga kita bisa berjalan mundur. Besarnya gaya aksi dan reaksi sama, tetapi arahnya berlawanan. Telapak kaki kita mendorong lantai ke belakang, lantai mendorong telapak kaki kita ke depan. Ketika kita berjalan lambat, gaya yang kita berikan kecil, sehingga gaya reaksi yang diberikan oleh lantai juga kecil, akibatnya kita berjalan pelan. Pada saat kita berjalan cepat, telapak kaki kita menekan lantai lebih kuat, akibatnya gaya reaksi yang diberikan lantai juga besar sehingga kita didorong dengan kuat ke depan. Dirimu dapat melakukan percobaan ini untuk membuktikannya. Ketika kita berlari, gaya aksi berupa dorongan yang diberikan oleh telapak kaki kita kepada permukaan tanah sangat besar sehingga gaya reaksi yang diberikan oleh permukaan tanah kepada telapak kaki kita juga sangat besar. Akibatnya kita bisa berlari dengan kencang. Jadi besarnya gaya reaksi yang diberikan oleh permukaan tanah atau lantai kepada telapak kaki kita sebanding alias sama besar dengan gaya aksi yang kita berikan dan arahnya berlawanan.
 Gas dikatakan melakukan usaha apabila volume gas bertambah besar (atau mengembang) dan V2 > V1. sebaliknya, gas dikatakan menerima usaha (atau usaha dilakukan terhadap gas) apabila volume gas mengecil atau V2 < V1 dan usaha gas bernilai negatif.
Gas dikatakan melakukan usaha apabila volume gas bertambah besar (atau mengembang) dan V2 > V1. sebaliknya, gas dikatakan menerima usaha (atau usaha dilakukan terhadap gas) apabila volume gas mengecil atau V2 < V1 dan usaha gas bernilai negatif.



Daptar eusi[sumputkeun] |
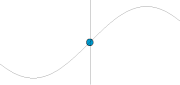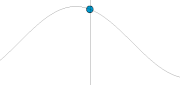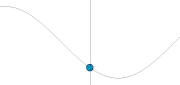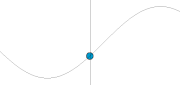

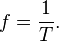






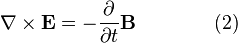


 ngarupakeun hiji operator diférensial véktor (tempo Del).
ngarupakeun hiji operator diférensial véktor (tempo Del). ,
,



 |
 . . |
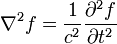
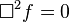
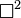 ngarupakeun d'Alembertian:
ngarupakeun d'Alembertian: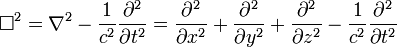


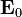 ngarupakeun amplitudo konstan, f ngarupakeun satiap fungsi anu bisa didiférensiasi,
ngarupakeun amplitudo konstan, f ngarupakeun satiap fungsi anu bisa didiférensiasi, 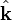 ngarupakeun hiji véktor unit dina arah rambatan, sarta
ngarupakeun hiji véktor unit dina arah rambatan, sarta  ngarupakeun hiji véktor posisi. Urang nempo yén
ngarupakeun hiji véktor posisi. Urang nempo yén  ngarupakeun hiji jawaban umum kana rumus gelombang. Dina kalimah lain
ngarupakeun hiji jawaban umum kana rumus gelombang. Dina kalimah lain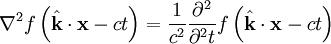 ,
,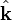 .
.
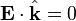


 .
. .
.