Ti Wikipédia, énsiklopédia bébas basa Sunda
Gelombang mangrupakeun hiji gangguan anu ngarambat ngaliwatan rohangan jeung waktu, sarta biasana dibarengan ku pamindahan énergi. Gelombang mékanik hadir dina hiji médium (mangsa lumangsung parobahan bentuk médium, mampuh ngahasilkeun gaya-gaya élastis nu ngabalikkeun deui bentuk ka asalna). Gelombang tina radiasi éléktromagnétik (sarta mungkin radiasi gravitasional) bisa ngarambat dina rohangan hapa, nyaéta tanpa médium. Gelombang ngaliwat sarta mindahkeun énergi ti hiji titik ka titik lianna, malah mindeng dibarengan ku saeutik pamindahan partikel médium atawa henteu permanén (nyaéta saeutik atawa tanpa pangangkutan massa); tapi aya osilasi di sabudeureun lokasi-lokasi tinangtu. Daptar eusi[sumputkeun] |
[édit] Gambaran sacara matematik
Ditingali tina matematika, gelombang anu paling primitif (atawa dasar) nyaeta gelombang harmonik (sinusoidal) anu digambarkeun ku rumus f(x,t) = Asin(wt-kx)), dimana A ngarupakeun amplitudo gelombang - sahiji ukuran gangguan maksimum dina jero midiyeum salila hiji siklus gelombang (jarak maksimum titik pangluhurna ti titk kasaimbangan). Dina ilustrasi di sabeulah katuhu, amplitudo ngarupakeun jarak vertikal maksimum antara garis dasar jeung gelombang. Unit amplitudo gumantung kana jinis gelombang— gelombang dawai miboga amplitudo anu dinyatakeun dina jarak (meter), gelombang sora dinyatakeun dina tekanan (pascals) sarta gelombang elektromagnetik dinyatakeun dina (volts/meter). Amplitudo bisa wae tetep (dina hal ieu gelombang ngarupakeun sahiji gelombang sinambungc.w. atawa continuous wave), atawa bisa oge robah-robah (variasi) nurutkeun waktu jeung / atawa posisi. Wangunan variasi amplitudo disebut amplop gelombang.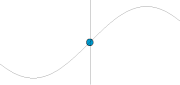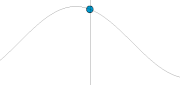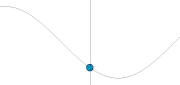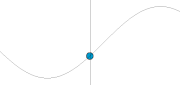
Gelombang bisa digambarkeun ku gerak harmonik saderhana.
[édit] Panjang gelombang
Panjang gelombang (dilambangkeun ku λ) ngarupakeun jarak antara dua puncak (atawa jurang) anu ngaréndéng. Panjang gelombang umumna boga hijian méter; gelombang cahaya dina spéktrum éléktromagnétik umumna diukur maké hijian ukuran panjang nanométer.Nomergelombang k bisa dikaitkeun jeung panjang gelombang ku rumus:
[édit] Périoda jeung frékuénsi
Artikel utama: Frékuénsi
Périoda T nyaéta waktu anu diperlukeun pikeun gelombang ngayun bulak-balik dina sahiji siklus. Frékuénsi f (oge mindeng dilambangkeun kuν) nyaéta sabaraha loba périoda per hijian waktu (contona dina sadetik) sarta dikur maké hijian hertz. Ieu dirumuskeun ku:[édit] Frékuénsi sudut
Frékuénsi sudut ω ngagambarkeun frékuénsi dina terminologi radian per detik. Frékuénsi sudut dihubungkeun jeung frékuénsi ku rumus:[édit] Gelombang éléktromagnétik
Gelombang éléktromagnétik (ÉM) nyaéta kabéh gelombang anu dihasilkeun tina interaksi antara médan listrik jeung médan magnét. Kumpulan gelombang ÉM ti mimiti nu panjangna rébuan kilométer tepi ka nu sapondok ukuran atom ngawangun spéktrum anu disebut spéktrum gelombang éléktromagnétik. Umumna disebutkeun yén gelombang ÉM anu panjangna di luar wates-wates kasebut henteu lumrah, sanajan anggapan ieu henteu sakabéhna bener. Wates gelombang pondok kamungkinan ngarupakeun gelombang Planck, ari wates paling panjang saukuran jeung jagat raya (tingali kosmologi fisika), sanajan dina dasarna spéktrum teh taya hinggana.Energi éléktromagnétik dina hiji panjang gelombang λ (dina rohangan bébas) miboga sahiji frékuénsi f jeung energi foton E. Jadi, spéktrum gelombang éléktromagnétik bisa dinyatakeun dina tilu kuantitas ieu. Katilu kuantitas ieu dihubungkeun ku rumus:
- laju gelombang (c) = frékuénsi x panjang gelombang
- c nyaéta laju cahaya, 299,792,458 m/s (pasti).
- h nyaéta konstanta Planck
Mangsa gelombang cahaya (jeung gelombang éléktromagnétik lianna) asup kana sahiji médiyeum, panjang gelombangna ngurangan. Panjang gelombang éléktromagnétik, teu paduli médiyeum naon anu diliwatanna, biasana dirumuskeun dikaitkeun jeung panjang gelombang dina rohangan bébas, sanajan hal ieu teu salawasna dinyatakeun sacara jelas.
Umumna, dumasar panjang gelombangna, gelombang ÉM digolongkeun kana gelombang-gelombang energi listrik, radio, gelombang mikro, infrabeureum, cahaya katémbong anu karasa ku urang sabagé cahaya, ultraviolét, sinar-X jeung sinar gamma.
[édit] Cahaya
- Artikel utama: cahaya
Serat optik ngarambatkeun cahaya anu bisa ditumpangan data sora atawa gambar. Prosésna sarupa jeung anu digunakeun dina ngarambatkeun gelombang radio.
[édit] Gelombang radio
- Artikel utama: frékuénsi radio
Mangsa rambatan gelombang ÉM asup kana konduktor, rambatan ÉM ngaraksuk kana konduktor, ngaliwatan, jeung ngabangkitkeun arus listrik dina beungeut konduktor ku cara ngagerakkeun éléktron-éléktron material konduktor. Éfék ieu (éfék kulit atawa skin effect) digunakeun dina anteneu. Pancaran gelombang ÉM ogé bisa ngabalukarkeun molékul-molékul nyerep energi jeung saterusna jadi panas; cara ieu digunakeun dina oven microwave.
[édit] Rumus-rumus Gelombang Éléktromagnétik
Gelombang éléktromagnétik salaku hiji fénomena umum ditorah ku hukum-hukum klasik ngeunaan listrik jeung magnétisme, anu katelah sabagé rumus-rumus Maxwell. Lamun urang mariksa rumus-rumus Maxwell tanpa sumber (muatan listrik atawa arus listrik) mangka urang bakal meunangkeun jawaban nontrivial tina médan listrik jeung médan magnét anu robah-robah. Dimimitian ku rumus Maxwell pikeun hiji rohangan hapa:-
- dimana
 ngarupakeun hiji operator diférensial véktor (tempo Del).
ngarupakeun hiji operator diférensial véktor (tempo Del).
-
 ,
,
Pikeun nempo hiji deui jawaban anu leuwih narik haté, urang ngagunakeun identitas véktor, anu lumaku pikeun satiap véktor, saperti kieu:
-
- dimana urang nyaderhanakeun anu di luhur ku cara ngagunakeun rumus (1).
-
-
 .
.
-
-
- dimana
- c ngarupakeun laju gelombang sarta
- f ngagambarkeun pamindahan tempat
-
- dimana
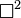 ngarupakeun d'Alembertian:
ngarupakeun d'Alembertian:
Tapi masih aya dua rumus Maxwell deui. Coba tempo hiji gelombang véktor umum pikeun médan listrik.
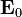 ngarupakeun amplitudo konstan, f ngarupakeun satiap fungsi anu bisa didiférensiasi,
ngarupakeun amplitudo konstan, f ngarupakeun satiap fungsi anu bisa didiférensiasi, 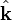 ngarupakeun hiji véktor unit dina arah rambatan, sarta
ngarupakeun hiji véktor unit dina arah rambatan, sarta  ngarupakeun hiji véktor posisi. Urang nempo yén
ngarupakeun hiji véktor posisi. Urang nempo yén  ngarupakeun hiji jawaban umum kana rumus gelombang. Dina kalimah lain
ngarupakeun hiji jawaban umum kana rumus gelombang. Dina kalimah lain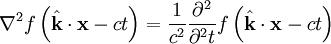 ,
,
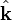 .
.Wangun ieu bakal ngajawab rumus gelombang, tapi naha ieu bakal ngajawab sakabéh rumus Maxwell, sarta médan magnét naon anu pakait?
 .
.Médan listrik jeung médan magnét sajaba ngarambat dina laju cahaya, ogé boga oriéntasi sarta gedé anu proporsional anu kawates, E0 = cB0, anu bisa ditempo langsung tina Poynting vector. Médan listrik, médan magnét, sarta arah rambatan gelombang kabéhanana ortogonal, sarta gelombang ngarambat dina arah anu sarua saperti
 .
.Lamun ditingali tina arah rambatan gelombang éléktromagnétik, médan listrik mungkin ngayunambing naék jeung turun, samentara médan magnét ngayunambing ka katuhu jeung ka kénca; tapi gambar éta bisa diputer sahingga médan listrik ngayunambing ka katuhu jeung ka kenca samentara médan magnét ngayunambing turun jeung naék. Hal ieu ngarupakeun jawaban lian pikeun gelombang anu ngarambat ka arah anu sarua. Kasambarangan oriéntasi ditingali ti arah rambatan disebut polarisasi.




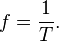




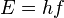



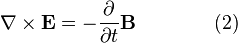







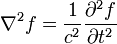
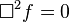
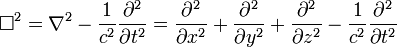



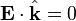



0 comments:
Posting Komentar