TEORI BILANGAN

• Teori bilangan (number theory) adalah teori yang mendasar dalam memahami algoritma kriptografi

• Bilangan yang dimaksudkan adalah bilangan bulat (integer)

BARISAN DAN DERET GEOMETRI {UKUR/KALI}

1. BARISAN GEOMETRI
   U₁, U₂, U₃, ......., U_n-1, U_n disebut barisan geometri, jika
   
   U₁/U₂ = U₃/U₂ = .... = U_n / U_n-1 = konstanta
   
   Konstanta ini disebut pembanding / rasio (r)Rasio r = U_n / U_n-1
   Suku ke-n barisan geometri
   
   a, ar, ar² , .......ar^n-1
   U₁, U₂, U₃,......,U_n
   
   Suku ke n U_n = ar^n-1 ® fungsi eksponen (dalam n)

BARISAN DAN DERET ARITMATIKA

BARISAN adalah urut-urutan bilangan dengan aturan tertentu. 
Suku-suku suatu barisan adalah nilai-nilai dari suatu fungsi yang daerah definisinya himpunan bilangan asli (n = natural = asli)
Contoh:

1. Un = 2n - 1
   adalah suku ke-n dari suatu barisan, dimana n Î N = {1,2,3,.....}
   Barisan itu adalah : 1,3,5,7,....
   
   
2. Diketahui barisan 1/3 , 1/6 , 1/9
   Rumus suku ke-n barisan ini adalah U_n = 1/3n

GEOMETRI TRANSFORMASI

Transformasi adalah suatu perpindaban/perubaban.

1. TRANSLASI (Pergeseran sejajar)
   

   Matriks	Perubahan	Perubahan
   é a ù ë bû	(x,y) ® (x+a, y+b)	F(x,y) = 0 ® (x-a, y-b) = 0
   Ket : x' = x + a ® x = x' - a y' = y + b ® y = y' -b

   Sifat:
   
   • Dua buah translasi berturut-turut é a ù diteruskan dengan 
                                                  ë b û
     dapat digantikan dengan é c ù translasi tunggal é a + c ù
                                      ë d û                       ë b + d û 
     
   • Pada suatu translasi setiap bangunnya tidak berubah.
     

BANGUN DATAR

1. Persegi Panjang


Persegi Panjang adalah segiempat yang keempat sudutnya siku - siku dan sisi - sisi yang
berhadapan sama panjang dan sejajar.
Sifat - sifat :
a. sisi yang berhadapan sama panjang dan sejajar
b. sudut - sudutnya sama besar yaitu sudut siku - siku = 90 derajat
c. Diagonal - diagonalnya sama panjang dan berpotongan serta saling mmembagi dua sama panjang.

• Rumus Persegi Panjang

Luas = p x l

Keliling = 2p + 2l = 2 x (p + l)

dengan p = panjang persegi panjang, dan l = lebar persegi panjang

2. Persegi

Persegi adalah persesgi panjang yang keempat sisinya sama panjang
Sifat - sifat :
a. sisi yang berhadapan sama panjang dan sejajar
b. sudut - sudutnya dibagi dua sama besar oleg diagonal,, sehingga diagonal - diagonalnya
merurpakan sumbu simetri.
c. Diaagonal - diagonalnya berpotongan membentukk sudut siku - siku = 90 derajat
Keliling = 4 x s
Luas = s x s
Panjang diagonal = sisi x akar 2


3. Jajargenjang

Jajargenjang dapat dibentuk dari gabungan sebuah segitiga dan bayanganya setelah diputar
setengah putaran dengan pusat titik tengah salah satu sisinya.
Sifat - sifat :
a. sisi yang berhadapan sama panjang dan sejajar
b. Sudut - sudut yang berhadapan sama besar
c. Jumlah besar sudut - sudut yang berdekatan adalah 180 derajat
d. Kedua diagonal saling membagi dua sama panjang.
Luas = alas x tinggi


4. Belah Ketupat

Belah ketupat dibentuk dari gabungan segitiga samakaki dan bayanganya setelah
dicerminkan terhadap alasnya
Sifat - sifat :
a. semua sisinya sama panjang
b. Sudut - sudut yang berhadapan sama besar dan dibagi dua sama besar oleh diagonal
diagonalnya
c. Kedua diagonal merupakan sumbu simetri
d. Kedua diagonal saling membagi dua sama panjang dan saling berpotongan tegak lurus.
Luas = 1/2 x diagonal 1 x diagonal 2


5. Layang - layang

Layang - layang dibentuk dari gabungan dua segitiga samakaki yang panjang alasnya sama
dan berhimpit.
Sifat - sifat :
a. masing - masing sepasang sisinya sama panjang
b. salah satu diagonalnya merupakan sumbu simteri
c. salah satu diagonalnya membagi dua sama panjang diagonal lain dan tegak lurus dengan
diagonal itu.
Luas = 1/2 x diagonal 1 x diagonal 2


6. Trapesium adalah segiempat dengan tepat sepasang sisi yang berhadapan sejajar.

Sifat - sifat : jumlah sudut yang berdekatan diantara dua sisi sejajar adalah 180 derajat.

SEJARAH NOL

                                                                    Sejarah Nol

Waclaw Sierpinski, seorang pakar Matematika yang cemerlang … cemas karena kehilangan sebuah tas bawaannya. “Tidak sayang!”, kata istrinya. “Semuanya ada enam di sini”. “Tidak mungkin”, Kata Sierpinski. “Aku telah menghitungnya berulang kali: nol, satu, dua, tiga, empat, lima.” – The Book Of Number.

Dalam sehari-hari, sesungguhnya kita tidak membutuhkan angka nol, benar-benar tidak butuh. Ketika anda ditanya, ‘Punya berapa jerukkah anda ?’, maka anda akan cenderung untuk mengatakan ‘Saya tidak punya jeruk’ ketimbang mengatakan ‘Saya mempunyai nol jeruk’. Ketika kita mempunyai seorang adik dan ditanya ‘Berapa tahun umur adikmu itu ?’. Maka kita lebih memilih untuk menjawab ‘Umurnya baru 1 bulan’ daripada harus menjawab dengan ’Umurnya baru 0 tahun’. Inilah masalahnya, karena dalam prakteknya kita sama sekali tidak memerlukan angka nol.

RUMUS LENGKAP FISIKA (kalor)

Kalor jenis

Rumus:

dengan ketentuan:

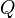• = Kalor yang diterima suatu zat (Joule, Kilojoule, Kalori, Kilokalori)
• = Massa zat (Gram, Kilogram)
• = Kalor jenis (Joule/kilogram°C, Joule/gram°C, Kalori/gram°C)
• = Perubahan suhu (°C) → (t₂ - t₁)