JIka A dan B matriks bujur sangkar sedemikian rupa sehingga A B = B A = I , maka B disebut balikan atau
invers dari A dan dapat dituliskan
B = A − 1 ( B sama dengan
invers A ). Matriks B juga mempunyai
invers yaitu A maka dapat dituliskan
A = B − 1. Jika tidak ditemukan matriks B, maka A dikatakan
matriks tunggal (singular). Jika matriks B dan C adalah
invers dari A maka B = C.
Matriks A =

dapat di-
invers apabila ad - bc ≠ 0
Dengan Rumus =
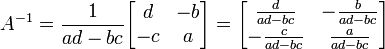
Apabila A dan B adalah matriks seordo dan memiliki balikan maka AB dapat di-
invers dan
(AB) − 1 = B − 1A − 1
Contoh 1:
Matriks
-
- A =
 dan B =
dan B = 
-
- AB =

 =
=  = I (matriks identitas)
= I (matriks identitas)
-
- BA =

 =
=  = I (matriks identitas)
= I (matriks identitas)
Maka dapat dituliskan bahwa
B = A − 1 (B Merupakan
invers dari A)
Contoh 2:
Matriks
-
- A =
 dan B =
dan B = 
-
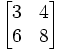
- AB =

 =
= 
-
- BA =

 =
= 
Karena AB ≠ BA ≠ I maka matriks A dan matriks B disebut
matriks tunggal.
Contoh 3:
Matriks
-
- A =

Tentukan Nilai dari A
-1
Jawab:

Contoh 4:
Matriks
-
- A =
 , B =
, B =  , AB =
, AB = 
Dengan menggunakan rumus, maka didapatkan
-
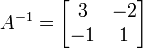 ,
, 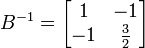 ,
, 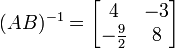
Maka
-

 =
= 
Ini membuktikan bahwa
(AB) − 1 = B − 1A − 1
 dapat di-invers apabila ad - bc ≠ 0
dapat di-invers apabila ad - bc ≠ 0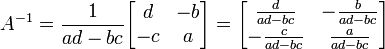
 dan B =
dan B = 

 =
=  = I (matriks identitas)
= I (matriks identitas)
 =
=  = I (matriks identitas)
= I (matriks identitas) dan B =
dan B = 

 =
= 

 =
= 


 , B =
, B =  , AB =
, AB = 
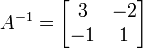 ,
, 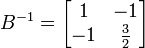 ,
, 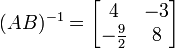

 =
= 

8 comments:
thank's atas infonya, tp lebih bagus lagi dikasih perincianya
misal, perkalian'a di silang atau dijelaskan rumus baku'a
sory cuma saran ^^
makasih gan buat infonya.. visit blog saya gan..
mlisunblog.blogspot.com
Gmn sih rumus matrika yang jelas, susah bgt nih soalnya
mksih infonya. lebih bgusnya d tmbah trik cepatnya kan ada juga tuh..
mksih :)
thanks gan ;)
Bisa ga si diperjelas lagi? Gamasuk otak tentang invers suwer-_-
makasih ya gan, ini saya lagi ulangan sangat membantu
Dik= x+y=2
3x+(-2y)=1
tentukan 2x+5y=
matriks AXB
Posting Komentar