Termodinamika adalah kajian tentang kalor (panas) yang berpindah. Dalam termodinamika kamu akan banyak membahas tentang sistem dan lingkungan. Kumpulan benda-benda yang sedang ditinjau disebut sistem, sedangkan semua yang berada di sekeliling (di luar) sistem disebut lingkungan.
Usaha Luar
Usaha luar dilakukan oleh sistem, jika kalor ditambahkan (dipanaskan) atau kalor dikurangi (didinginkan) terhadap sistem. Jika kalor diterapkan kepada gas yang menyebabkan perubahan volume gas, usaha luar akan dilakukan oleh gas tersebut. Usaha yang dilakukan oleh gas ketika volume berubah dari volume awal V1 menjadi volume akhir V2 pada tekanan p konstan dinyatakan sebagai hasil kali tekanan dengan perubahan volumenya.
W = p∆V= p(V2 – V1)
Secara umum, usaha dapat dinyatakan sebagai integral tekanan terhadap perubahan volume yang ditulis sebagai
 Gas dikatakan melakukan usaha apabila volume gas bertambah besar (atau mengembang) dan V2 > V1. sebaliknya, gas dikatakan menerima usaha (atau usaha dilakukan terhadap gas) apabila volume gas mengecil atau V2 < V1 dan usaha gas bernilai negatif.
Gas dikatakan melakukan usaha apabila volume gas bertambah besar (atau mengembang) dan V2 > V1. sebaliknya, gas dikatakan menerima usaha (atau usaha dilakukan terhadap gas) apabila volume gas mengecil atau V2 < V1 dan usaha gas bernilai negatif.Energi Dalam
Suatu gas yang berada dalam suhu tertentu dikatakan memiliki energi dalam. Energi dalam gas berkaitan dengan suhu gas tersebut dan merupakan sifat mikroskopik gas tersebut. Meskipun gas tidak melakukan atau menerima usaha, gas tersebut dapat memiliki energi yang tidak tampak tetapi terkandung dalam gas tersebut yang hanya dapat ditinjau secara mikroskopik.
Berdasarkan teori kinetik gas, gas terdiri atas partikel-partikel yang berada dalam keadaan gerak yang acak. Gerakan partikel ini disebabkan energi kinetik rata-rata dari seluruh partikel yang bergerak. Energi kinetik ini berkaitan dengan suhu mutlak gas. Jadi, energi dalam dapat ditinjau sebagai jumlah keseluruhan energi kinetik dan potensial yang terkandung dan dimiliki oleh partikel-partikel di dalam gas tersebut dalam skala mikroskopik. Dan, energi dalam gas sebanding dengan suhu mutlak gas. Oleh karena itu, perubahan suhu gas akan menyebabkan perubahan energi dalam gas. Secara matematis, perubahan energi dalam gas dinyatakan sebagai
untuk gas monoatomik
untuk gas diatomik
Dimana ∆U adalah perubahan energi dalam gas, n adalah jumlah mol gas, R adalah konstanta umum gas (R = 8,31 J mol−1 K−1, dan ∆T adalah perubahan suhu gas (dalam kelvin).
Hukum I Termodinamika
Jika kalor diberikan kepada sistem, volume dan suhu sistem akan bertambah (sistem akan terlihat mengembang dan bertambah panas). Sebaliknya, jika kalor diambil dari sistem, volume dan suhu sistem akan berkurang (sistem tampak mengerut dan terasa lebih dingin). Prinsip ini merupakan hukum alam yang penting dan salah satu bentuk dari hukum kekekalan energi.
Gambar
Sistem yang mengalami perubahan volume akan melakukan usaha dan sistem yang mengalami perubahan suhu akan mengalami perubahan energi dalam. Jadi, kalor yang diberikan kepada sistem akan menyebabkan sistem melakukan usaha dan mengalami perubahan energi dalam. Prinsip ini dikenal sebagai hukum kekekalan energi dalam termodinamika atau disebut hukum I termodinamika. Secara matematis, hukum I termodinamika dituliskan sebagai
Q = W + ∆U
Dimana Q adalah kalor, W adalah usaha, dan ∆U adalah perubahan energi dalam. Secara sederhana, hukum I termodinamika dapat dinyatakan sebagai berikut.
Jika suatu benda (misalnya krupuk) dipanaskan (atau digoreng) yang berarti diberi kalor Q, benda (krupuk) akan mengembang atau bertambah volumenya yang berarti melakukan usaha W dan benda (krupuk) akan bertambah panas (coba aja dipegang, pasti panas deh!) yang berarti mengalami perubahan energi dalam ∆U.
Proses Isotermik
Suatu sistem dapat mengalami proses termodinamika dimana terjadi perubahan-perubahan di dalam sistem tersebut. Jika proses yang terjadi berlangsung dalam suhu konstan, proses ini dinamakan proses isotermik. Karena berlangsung dalam suhu konstan, tidak terjadi perubahan energi dalam (∆U = 0) dan berdasarkan hukum I termodinamika kalor yang diberikan sama dengan usaha yang dilakukan sistem (Q = W).
Proses isotermik dapat digambarkan dalam grafik p – V di bawah ini. Usaha yang dilakukan sistem dan kalor dapat dinyatakan sebagai

Proses Isokhorik
Jika gas melakukan proses termodinamika dalam volume yang konstan, gas dikatakan melakukan proses isokhorik. Karena gas berada dalam volume konstan (∆V = 0), gas tidak melakukan usaha (W = 0) dan kalor yang diberikan sama dengan perubahan energi dalamnya. Kalor di sini dapat dinyatakan sebagai kalor gas pada volume konstan QV.
QV = ∆U
Proses Isobarik
Jika gas melakukan proses termodinamika dengan menjaga tekanan tetap konstan, gas dikatakan melakukan proses isobarik. Karena gas berada dalam tekanan konstan, gas melakukan usaha (W = p∆V). Kalor di sini dapat dinyatakan sebagai kalor gas pada tekanan konstan Qp. Berdasarkan hukum I termodinamika, pada proses isobarik berlaku
QV =∆U
Dari sini usaha gas dapat dinyatakan sebagai
W = Qp − QV
Jadi, usaha yang dilakukan oleh gas (W) dapat dinyatakan sebagai selisih energi (kalor) yang diserap gas pada tekanan konstan (Qp) dengan energi (kalor) yang diserap gas pada volume konstan (QV).

Proses Adiabatik
Dalam proses adiabatik tidak ada kalor yang masuk (diserap) ataupun keluar (dilepaskan) oleh sistem (Q = 0). Dengan demikian, usaha yang dilakukan gas sama dengan perubahan energi dalamnya (W = ∆U).
Jika suatu sistem berisi gas yang mula-mula mempunyai tekanan dan volume masing-masing p1 dan V1 mengalami proses adiabatik sehingga tekanan dan volume gas berubah menjadi p2 dan V2, usaha yang dilakukan gas dapat dinyatakan sebagai

Proses adiabatik dapat digambarkan dalam grafik p – V dengan bentuk kurva yang mirip dengan grafik p – V pada proses isotermik namun dengan kelengkungan yang lebih curam.





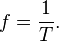




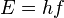



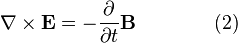


 ngarupakeun hiji operator diférensial véktor (tempo
ngarupakeun hiji operator diférensial véktor (tempo  ,
,




 .
.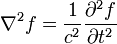
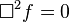
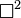 ngarupakeun
ngarupakeun 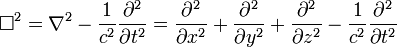


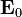 ngarupakeun amplitudo konstan,
ngarupakeun amplitudo konstan, 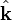 ngarupakeun hiji véktor unit dina arah rambatan, sarta
ngarupakeun hiji véktor unit dina arah rambatan, sarta  ngarupakeun hiji véktor posisi. Urang nempo yén
ngarupakeun hiji véktor posisi. Urang nempo yén  ngarupakeun hiji jawaban umum kana rumus gelombang. Dina kalimah lain
ngarupakeun hiji jawaban umum kana rumus gelombang. Dina kalimah lain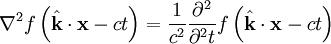 ,
,
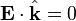


 .
. .
.