Pages
Followers
Labels
- berita unik (1)
- biologi (16)
- fisika (19)
- kata cinta (1)
- kimia (17)
- Matematika (24)
Total Tayangan Halaman
Subscribe to our feed
HUKUM ARCHIMEDES
Archimedes dari Syracusa (sekitar 287 SM - 212 SM) Ia belajar di kota Alexandria, Mesir. Pada waktu itu yang menjadi raja di Sirakusa adalah Hieron II, sahabat Archimedes. Archimedes sendiri adalah seorang matematikawan, astronom, filsuf, fisikawan, dan insinyur berbangsa Yunani. Ia dibunuh oleh seorang prajurit Romawi pada penjarahan kota Syracusa, meskipun ada perintah dari jendral Romawi, Marcellus bahwa ia tak boleh dilukai. Sebagian sejarahwan matematika memandang Archimedes sebagai salah satu matematikawan terbesar sejarah, mungkin bersama-sama Newton dan Gauss
Hukum Archimedes
Hukum Archimedes mengatakan bahwa "Jika suatu benda dicelupkan ke dalam sesuatu zat cair, maka benda itu akan mendapat tekanan keatas yang sama besarnya dengan beratnya zat cair yang terdesak oleh benda tersebut".
HUKUM-HUKUM NEWTON
Hukum pertama Newton : Hukum Inersia
Hukum ini juga disebut hukum inersia atau prinsip Galileo
''Jika resultan gaya pada suatu benda sama dengan nol, maka benda yang mula-mula diam akan terus diam. Sedangkan, benda yang mula-mula bergerak, akan terus bergerak dengan kecepatan tetap''
Hukum Newton I dapat diinterpretasikan sebagai berikut :
- Sebuah benda, akan tetap berada dalam keadaan diam atau akan terus bergerak, kecuali jika dipaksa berubah dengan menerapkan gaya luar ke benda tersebut
Pernyataan tersebut dapat dinyatakan dengan 
Keterangan :
- Sebuah benda akan tetap diam, atau bergerak dalam garis lurus dengan kecepatan tetap, kecuali diberi gaya luar.
Pernyataan tersbut, dalam notasi kalkulus, dapat dinyatakan dengan 
Keterangan :
 adalah diferensial kecapatan terhadap waktu
adalah diferensial kecapatan terhadap waktu
Hukum Newton I menjelaskan kerangka acuan di mana hukum II dan hukum III Newton dapat dibuktikan benar. Kerangka acuan ini disebut kerangka acuan inersial atau kerangka acuan Galilean.
Perkembangan hukum I Newton
Perkembangan hukum ini dapat ditelusuri hingga Aristoteles. Aristoteles membagi gerak menjadi dua, yaitu gerak alami dan gerak paksa, dalam hal gerak alami, menurutnya setiap benda akan mencari keadaan alaminya (eg. benda berat jatuh kebawah, benda ringan terbang keatas) dan menyatakan bahwa gerak melingkar adalah gerak alami yang tidak disebabkan oleh gaya. Dalam hal gerak paksa, Aristoteles berpendapat bahwa gerak paksa disebabkan oleh gaya luar yang bekerja pada suatu benda dan jika pada suatu benda tidak bekerja gaya luar, maka benda tersebut akan kembali ke keadaan alaminya yaitu diam.
Setelah Aristoteles, Galileo melakukan percobaan sendiri mengenai gerak dengan menggunakan bola dan menyimpulkan bahwa bola yang bergerak akan diperlambat kelajuannya sampai berhenti oleh gaya gesek. Pengamatan dan kesimpulan Galileo kemudian dipelajari dan dikembangkan oleh Newton untuk menyusun hukum pertamanya.
Jika suatu gaya total bekerja pada benda, maka benda akan mengalami percepatan, di mana arah percepatan sama dengan arah gaya total yang bekerja padanya. Vektor gaya total sama dengan massa benda dikalikan dengan percepatan benda.

m adalah massa benda dan a adalah (vektor) percepatannya. Jika persamaan di atas ditulis dalam bentuk a = F/m, tampak bahwa percepatan sebuah benda berbanding lurus dengan resultan gaya yang bekerja padanya dan arahnya sejajar dengan gaya tersebut. Tampak juga bahwa percepatan berbanding terbalik dengan massa benda.

Jadi apabila tidak ada gaya total alias resultan gaya yang bekerja pada benda maka benda akan diam apabila benda tersebut sedang diam; atau benda tersebut bergerak dengan kecepatan tetap, jika benda sedang bergerak. Ini merupakan bunyi Hukum I Newton.
Setiap gaya F merupakan vektor yang memiliki besar dan arah. Persamaan hukum II Newton di atas dapat ditulis dalam bentuk komponen pada koordinat xyz alias koordinat tiga dimensi, antara lain :

Satuan massa adalah kilogram, satuan percepatan adalah kilogram meter per sekon kuadrat (kg m/s2). Satuan Gaya dalam Sistem Internasional adalah kg m/s2. Nama lain satuan ini adalah Newton; diberikan untuk menghargai jasa eyang Isaac Newton. Satuan-satuan tersebut merupaka satuan Sistem Internasional (SI). Dengan kata lain, satu Newton adalah gaya total yang diperlukan untuk memberikan percepatan sebesar 1 m/s2 kepada massa 1 kg. Hal ini berarti 1 Newton = 1 kg m/s2.
Dalam satuan CGS (centimeter, gram, sekon), satuan massa adalah gram (g), gaya adalah dyne. Satu dyne didefinisikan sebagai gaya total yang diperlukan untuk memberi percepatan sebesar 1 cm/s2 untuk benda bermassa 1 gram. Jadi 1 dyne = 1 gr cm/s2.
Kedua jenis satuan yang kita bahas di atas adalah satuan Sistem Internasional (SI). Untuk satuan Sistem Inggris (British Sistem), satuan gaya adalah pound (lb). 1 lb = 4,45 N. Satuan massa = slug. Dengan demikian, 1 pound didefinisikan sebagai gaya total yang diperlukan untuk memberi percepatan sebesar 1 ft/s2 kepada benda bermassa 1 slug.
Dalam perhitungan, sebaiknya anda menggunakan satuan MKS (meter, kilogram, sekon) SI. Jadi jika diketahui satuan dalam CGS atau sistem British, terlebih dahulu anda konversi.
HUKUM III NEWTON
Apabila sebuah benda memberikan gaya kepada benda lain, maka benda kedua memberikan gaya kepada benda yang pertama. Kedua gaya tersebut memiliki besar yang sama tetapi berlawanan arah.
Secara matematis Hukum III Newton dapat ditulis sebagai berikut :
F A ke B = – F B ke A
F A ke B adalah gaya yang diberikan oleh benda A kepada benda B, sedangkan F B ke A adalah gaya yang yang diberikan benda B kepada benda A. Misalnya ketika anda menendang sebuah batu, maka gaya yang anda berikan adalah F A ke B, dan gaya ini bekerja pada batu. Gaya yang diberikan oleh batu kepada kaki anda adalah – F B ke A. Tanda negatif menunjukkan bahwa arah gaya reaksi tersebut berlawanan dengan gaya aksi yang anda berikan. Jika anda menggambar tanda panah yang melambangkan interaksi kedua gaya ini, maka gaya F A ke B digambar pada batu, sedangkan gaya yang diberikan batu kepada kaki anda, – F B ke A, digambarkan pada kaki anda.
Persamaan Hukum III Newton di atas juga bisa kita tulis sebagai berikut :
Faksi = -Freaksi
Hukum warisan eyang Newton ini dikenal dengan julukan hukum aksi-reaksi. Ada aksi maka ada reaksi, yang besarnya sama dan berlawanan arah. Kadang-kadang kedua gaya tersebut disebut pasangan aksi-reaksi. Ingat bahwa kedua gaya tersebut (gaya aksi-gaya reaksi) bekerja pada benda yang berbeda. Berbeda dengan Hukum I Newton dan Hukum II Newton yang menjelaskan gaya yang bekerja pada benda yang sama.
Gaya aksi dan reaksi adalah gaya kontak yang terjadi ketika kedua benda bersentuhan. Walaupun demikian, Hukum III Newton juga berlaku untuk gaya tak sentuh, seperti gaya gravitasi yang menarik buah mangga kesayangan anda. Ketika kita menjatuhkan batu, misalnya, antara bumi dan batu saling dipercepat satu dengan lain. batu bergerak menuju ke permukaan bumi, bumi juga bergerak menuju batu. Gaya total yang bekerja pada bumi dan batu besarnya sama. Bumi bergerak ke arah batu yang jatuh ? masa sich… karena massa bumi sangat besar maka percepatan yang dialami bumi sangat kecil (Ingat hubungan antara massa dan percepatan pada persamaan hukum II Newton). Walaupun secara makroskopis tidak tampak, tetapi bumi juga bergerak menuju batu atau benda yang jatuh akibat gravitasi. Bumi menarik batu, batu juga membalas gaya tarik bumi, di mana besar gaya tersebut sama namun arahnya berlawanan.
Hukum III Newton dalam Kehidupan Sehari-hari
Konsep Hukum III Newton sebenarnya sering kita alami dalam kehidupan sehari-hari, walau kadang tidak kita sadari. Hal apa saja dalam kehidupan sehari-hari yang menggunakan konsep Hukum III Newton ?
Hukum III Newton berlaku ketika kita berjalan atau berlari
Ketika berjalan, telapak kaki kita memberikan gaya aksi dengan mendorong permukaan tanah atau lantai ke belakang. Permukaan tanah atau lantai memberikan gaya reaksi kepada kita dengan mendorong telapak kaki kita ke depan, sehingga kita berjalan ke depan. Ketika berjalan mundur, telapak kaki kita mendorong permukaan tanah atau lantai ke depan. Sebagai reaksi, permukaan tanah atau lantai mendorong telapak kaki kita ke belakang sehingga kita bisa berjalan mundur. Besarnya gaya aksi dan reaksi sama, tetapi arahnya berlawanan. Telapak kaki kita mendorong lantai ke belakang, lantai mendorong telapak kaki kita ke depan. Ketika kita berjalan lambat, gaya yang kita berikan kecil, sehingga gaya reaksi yang diberikan oleh lantai juga kecil, akibatnya kita berjalan pelan. Pada saat kita berjalan cepat, telapak kaki kita menekan lantai lebih kuat, akibatnya gaya reaksi yang diberikan lantai juga besar sehingga kita didorong dengan kuat ke depan. Dirimu dapat melakukan percobaan ini untuk membuktikannya. Ketika kita berlari, gaya aksi berupa dorongan yang diberikan oleh telapak kaki kita kepada permukaan tanah sangat besar sehingga gaya reaksi yang diberikan oleh permukaan tanah kepada telapak kaki kita juga sangat besar. Akibatnya kita bisa berlari dengan kencang. Jadi besarnya gaya reaksi yang diberikan oleh permukaan tanah atau lantai kepada telapak kaki kita sebanding alias sama besar dengan gaya aksi yang kita berikan dan arahnya berlawanan.
STRUKTUR ATOM - KIMIA
Struktur atom merupakan satuan dasar materi yang terdiri dari inti atom beserta awan elektron bermuatan negatif yang mengelilinginya. Inti atom mengandung campuran proton yang bermuatan positif dan neutron yang bermuatan netral (terkecuali pada Hidrogen-1 yang tidak memiliki neutron). Elektron-elektron pada sebuah atom terikat pada inti atom oleh gaya elektromagnetik. Demikian pula sekumpulan atom dapat berikatan satu sama lainnya membentuk sebuah molekul. Atom yang mengandung jumlah proton dan elektron yang sama bersifat netral, sedangkan yang mengandung jumlah proton dan elektron yang berbeda bersifat positif atau negatif dan merupakan ion. Atom dikelompokkan berdasarkan jumlah proton dan neutron pada inti atom tersebut. Jumlah proton pada atom menentukan unsur kimia atom tersebut, dan jumlah neutron menentukan isotop unsur tersebut.
Istilah atom berasal dari Bahasa Yunani, yang berarti tidak dapat dipotong ataupun sesuatu yang tidak dapat dibagi-bagi lagi. Konsep atom sebagai komponen yang tak dapat dibagi-bagi lagi pertama kali diajukan oleh para filsuf India dan Yunani. Pada abad ke-17 dan ke-18, para kimiawan meletakkan dasar-dasar pemikiran ini dengan menunjukkan bahwa zat-zat tertentu tidak dapat dibagi-bagi lebih jauh lagi menggunakan metode-metode kimia. Selama akhir abad ke-19 dan awal abad ke-20, para fisikawan berhasil menemukan struktur dan komponen-komponen subatom di dalam atom, membuktikan bahwa 'atom' tidaklah tak dapat dibagi-bagi lagi. Prinsip-prinsip mekanika kuantum yang digunakan para fisikawan kemudian berhasil memodelkan atom.
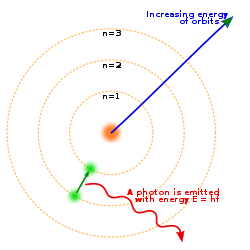
Relatif terhadap pengamatan sehari-hari, atom merupakan objek yang sangat kecil dengan massa yang sama kecilnya pula. Atom hanya dapat dipantau menggunakan peralatan khusus seperti mikroskop penerowongan payaran. Lebih dari 99,9% massa atom berpusat pada inti atom, dengan proton dan neutron yang bermassa hampir sama. Setiap unsur paling tidak memiliki satu isotop dengan inti yang tidak stabil yang dapat mengalami peluruhan radioaktif. Hal ini dapat mengakibatkan transmutasi yang mengubah jumlah proton dan neutron pada inti. Elektron yang terikat pada atom mengandung sejumlah aras energi, ataupun orbital, yang stabil dan dapat mengalami transisi di antara aras tersebut dengan menyerap ataupun memancarkan foton yang sesuai dengan perbedaan energi antara aras. Elektron pada atom menentukan sifat-sifat kimiawi sebuah unsur dan memengaruhi sifat-sifat magnetis atom tersebut.
Perkembangan Model Atom
Seorang filsuf Yunani yang bernama Democritus berpendapat bahwa jika suatu benda dibelah terus menerus, maka pada saat tertentu akan didapat akan didapat bagian yang tidak dapat dibelah lagi. Bagian seperti ini oleh Democritus disebut atom. Istilah atom berasal dari bahasa yunani “a” yang artinya tidak, sedangkan “tomos” yang artinya dibagi. Jadi, atom artinya tidak dapat dibagi lagi. Pengertian ini kemudian disempurnakan menjadi, atom adalah bagian terkecil dari suatu unsur yang tidak dapat dibelah lagi namun namun masih memiliki sifat kimia dan sifat fisika benda asalnya.
Atom dilambangkan dengan ZXA , dimana A = nomor massa (menunjukkan massa atom, merupakan jumlah proton dan neutron), Z = nomor atom (menunjukkan jumlah elektron atau proton). Proton bermuatan positif, neutron tidak bermuatan (netral), dan elektron bermuatan negatif. Massa proton = massa neutron = 1.800 kali massa elektron. .Atom-atom yang memiliki nomor atom sama dan nomor massa berbeda disebut isotop, atom-atom yang memiliki nomor massa sama dan nomor atom berbeda dinamakan isobar, atom-atom yang memiliiki jumlah neutron yang sama dinamakan isoton.
Macam-macam Model Atom
1. Model Atom John Dalton
Pada tahun 1808, John Dalton adalah seorang guru di Inggris yang melakukan perenungan tentang atom. Hasil perenungan Dalton menyempurnakan teori atom Democritus. Bayangan Dalton dan Democritus adalah bahwa benda itu berbentuk pejal. Dalam perenungannya Dalton mengemukakan postulatnya tentang atom.
a. Setiap unsur terdiri dari partikel yang sangat keci yang dinamakan dengan atom
b. Atom dari unsur yang sama memiliiki sifat yang sama
c. Atom dari unsur berbeda memiliki sifat yang berbeda pula
d. Atom dari suatu unsur tidak dapat diubah menjadi atom unsur lain dengan reaksi kimia, atom tidak dapat dimusnahkan dan atom juga tidak dapat dihancurkan
e. Atom-atom dapat bergabung membentuk gabungan atom yang disebut molekul
f. Dalam senyawa, perbandingan massa masing-masing unsur adalah tetap
Kelebihan model atom Dalton:
Mulai membangkitkan minat terhadap penelitian mengenai model atom.
Kelemahan model atom John Dalton :
Teori atom Dalton tidak dapat menerangkan suatu larutan dapat menghantarkan arus listrik. Bagaimana mungkin bola pejal dapat menghantarkan arus listrik? padahal listrik adalah elektron yang bergerak. Berarti ada partikel lain yang dapat menghantarkan arus listrik.
2. Model Atom J.J. Thomson
Pada tahun 1897, J.J Thomson mengamati elektron. Dia menemukan bahwa semua atom berisi elektron yang bermuatan negatif. Dikarenakan atom bermuatan netral, maka setiap atom harus berisikan partikel bermuatan positif agar dapat menyeimbangkan muatan negatif dari elektron.
Kelebihan model atom Thomson
Membuktikan adanya partikel lain yang bermuatan negatif dalam atom. Berarti atom bukan merupakan bagian terkecil dari suatu unsur.
Kelemahan model atom Thomson
Model Thomson ini tidak dapat menjelaskan susunan muatan positif dan negatif dalam bola atom tersebut.
3. Model Atom Rutherford
Rutherford melakukan penelitian tentang hamburan sinar α pada lempeng emas. Hasil pengamatan tersebut dikembangkan dalam hipotesis model atom Rutherford.
a. Sebagian besar dari atom merupakan permukaan kosong.
b. Atom memiliki inti atom bermuatan positif yang merupakan pusat massa atom.
c. Elektron bergerak mengelilingi inti dengan kecepatan yanga sangat tinggi.
d. Sebagian besar partikel α lewat tanpa mengalami pembelokkan/hambatan. Sebagian kecil dibelokkan, dan sedikit sekali yang dipantulkan.
Kelemahan Model Atom Rutherford
a. Menurut hukum fisika klasik, elektron yang bergerak mengelilingi inti memancarkan energi dalam bentuk gelombang elektromagnetik. Akibatnya, lama-kelamaan elektron itu akan kehabisan energi dan akhirnya menempel pada inti.
b. Model atom rutherford ini belum mampu menjelaskan dimana letak elektron dan cara rotasinya terhadap ini atom.
c. Elektron memancarkan energi ketika bergerak, sehingga energi atom menjadi tidak stabil.
d. Tidak dapat menjelaskan spektrum garis pada atom hidrogen (H).
4. Model Atom Niels Bohr
Pada tahun 1913, Niels Bohr mengemukakan pendapatnya bahwa elektron bergerak mengelilingi inti atom pada lintasan-lintasan tertentu yang disebut kulit atom. Model atom Bohr merupakan penyempurnaan dari model atom Rutherford.
Kelemahan teori atom Rutherford diperbaiki oleh Neils Bohr dengan postulat bohr :
a. Elektron-elektron yang mengelilingi inti mempunyai lintasan dan energi tertentu.
b. Dalam orbital tertentu, energi elektron adalah tetap. Elektron akan menyerap energi jika berpindah ke orbit yang lebih luar dan akan membebaskan energi jika berpindah ke orbit yang lebih dalam
Kelebihan model atom Bohr
atom terdiri dari beberapa kulit untuk tempat berpindahnya elektron.
Kelemahan model atom Bohr
a. tidak dapat menjelaskan efek Zeeman dan efek Strack.
b. Tidak dapat menerangkan kejadian-kejadian dalam ikatan kimia dengan baik, pengaruh medan magnet terhadap atom-atom, dan spektrum atom yang berelektron lebih banyak.
KIMIA {KELARUTAN & HASIL KALI KELARUTAN}
Untuk memahami hal tersebut, lakukanlah kegiatan berikut!
- Ambil 10 g kristal NaCl (garam dapur), kemudian masukkan ke dalam 50 mL air. Aduk hingga larut. Masukkan lagi 10 g NaCl dan diaduk. Ulangi terus sampai NaCl tidak dapat larut. Catat berapa gram NaCl yang ditambahkan.
- Ulangi percobaan di atas dengan air panas bertemperatur 50, 70, dan 90 °C. Catat hasilnya.
- Buat grafik temperatur vs kelarutan (g terlarut/50 mL air)
- Dari hasil percobaan, diskusikan dengan teman kelompok!
- Garam AB larut semua lalu jika ditambah garam AB lagi masih dapat larut ĺ larutan tak jenuh.
- Garam AB larut semua lalu jika ditambah garam AB lagi tidak dapat larut ĺ larutan jenuh.
- Garam AB larut sebagian ĺ larutan kelewat jenuh.
Contoh :

Bila Ksp AgCl = 10-10 , maka berarti larutan jenuh AgCl dalam air pada suhu 25 oC, Mempunyai nilai [Ag+] [Cl-] = 10-10
Kelarutan
1. Kelarutan zat AB dalam pelarut murni (air).
keterangan: s = kelarutan
Kelarutan tergantung pada :
- Suhu
- pH larutan
- Ion sejenis
AB(s) → A+ (aq) + B- aq)
s → n.s s
Larutan AX :
AX(aq) → A+(aq) + X-(aq)
b → b b
maka dari kedua persamaan reaksi di atas: [A+] = s + b = b, karena nilai s cukup kecil bila dibandingkan terhadap nilai b sehingga dapat diabaikan. B-1] = s
Jadi : Ksp AB = b . s
Contoh :
Bila diketahui Ksp AgCl = 10-10, berapa mol kelarutan (s) maksimum AgCl dalam 1 liter larutan 0.1 M NaCl ?
Jawab:
AgCl(s) → Ag+(aq) + Cl-(aq)
s → s s
NaCl(aq) ĺ Na+(aq) + Cl-(aq)
Ksp AgCl = [Ag+] [Cl-]
= s . 10-1
Maka,
s = 10-10/10-1
= 10-9 mol/liter
Dari contoh di atas kita dapat menarik kesimpulan bahwa makin besar konsentrasi ion sojenis maka makin kecil kelarutan elektrolitnya.
a. Pembentukan garam-garam.
- [A+] x [B-] < Ksp →
Apakah terjadi pengendapan CaCO3. jika ke dalam 1 liter 0.05 M Na2CO3 ditambahkan 1 liter 0.02 M CaCl2, dan diketahui harga Ksp untuk CaCO3 adalah 10-6.
Jawab :

maka :
[Ca2+] x [CO32-] = 2.5 x 10-2 x 10-2
[Ca2+] x [CO32-] > Ksp CaCO3, maka akan terjadi endapan CaCO3
LIMIT TRIGONOMETRI
Untuk x <<< ( x ® 0 ) maka sin x » x
(x <<< kecil sekali ; » setara )
l i m sin x = 1 l i m tg x = 1
x ® 0 x x ® 0 x
l i m x = 1 l i m x = 1
x ® 0 sin x x ® 0 tg x
PERLUASAN
l i m sin ax = a/b l i m tg ax = a/b
x ® 0 bx x ® 0 bx
l i m ax = a/b l i m ax = a/b
x ® 0 sin bx x ® 0 tg bx
l i m sin ax = a/b l i m tg ax = a/b
x ® 0 sin bx x ® 0 tg bx
l i m sin ax = a/b l i m tg ax = a/b
x ® 0 tg bx x ® 0 sin bx
Rumus-rumus trigonometri yang sering digunakan untuk merubah fungsi:
cos x = sin (90° - x)
ctg x = tg (90° - x)
sin ax = 2 sin ½ax cos ½ax
cos ax = 1- 2 sin² ½ax
cos²x = 1 - sin²x
HAL-HAL KHUSUS
| l i m axm + bxm-1 + .... = x ® ¥ pxn + qxn-1 + ... | ¥ untuk m > n ; a/p untuk m =n ; 0 untuk m < n |
| l i m Öax2 + bx + c - Ödx2 + ex + f x ® ¥ | ¥ untuk a > d ; b-e untuk m =n ; 2Öa -¥ untuk a < d |
DALIL L'HOSPITAL
Jika fungsi f dan g masing-masing terdifferensir pada titik x= a
dan f(a) = g(a) = 0 atau f(a) = g(a) = ¥ maka
l i m f(x) = l i m f(x)
x ® ¥ g(x) x ® a g(x)
CONTOH LIMIT FUNGSI ALJABAR
1. l i m x2 - 5x + 6 = (3)2 - 5(3) + 6 = 0
x ® 3
2. l i m 3x - 2 = ¥ (*) Uraikan
x ® ¥ 2x + 1 ¥
x(3 - 2/x) = 3 - 2/x = 3 - 0 = 3
x(2 - 1/x) 2 + 1/x 2 - 0 2
atau langsung gunakan hal khusus
3. l i m x2 - x - 1 = ¥ (*) Uraikan
x ® ¥ 10x + 9 ¥
x(x - 1 - 1/x) = x - 1 - 1/x = ¥ - 1 - 0 = ¥ =¥
x(10 - 9/x) 10 + 9/x 10 + 0 10
atau langsung gunakan hal khusus
4. l i m x2 - 3x + 2 = 0 (*) Uraikan
x ® 2 x2 - 5x + 6 0
(x - 1)(x - 2) = (x - 1) = 2 - 1 = -1
(x - 3)(x - 2) = (x - 3) = 2 - 3
atau langsung gunakan hal khusus ® Differensial
5. l i m x3 - 3x2 + 3x - 1 = 0 (*) Uraikan
x ® 1 x2 - 5x + 6 0
(x - 1)3 = (x - 1)2 = (1 - 1)2 = 0
(x - 1) (x - 5) (x + 5) (1 + 5) 6
atau langsung gunakan hal khusus ® Differensial
6. l i m Ö2 + x - Ö2x = 0 (*) Hilangkan tanda akar dengan
x ® 2 x - 2 0 mengalikan bentuk sekawan
(x - 1)3 = (x - 1)2 = (1 - 1)2 = 0 = 0
(x - 1) (x - 5) (x + 5) (1 + 5) 6
atau langsung gunakan hal khusus ® Differensial
7. l i m (3x - Ö9x2 + 4x) = ¥ - ¥ (*) Hilangkan tanda akar
x ® ¥
l i m (3x - Ö9x2 + 4x ) = é 3x - Ö9x2 + 4x ù = (*) Hilangkan tanda
x ® ¥
l i m (9x2 - (9x2 + 4x) = l i m -4x =
x ® ¥ 3x + Ö(9x2 + 4x) x ® ¥ 3x + 3x Ö[1+(a/9x)]
l i m -4 = -4 = -2
x ® ¥ 3 + 3Ö(1 + 0) 6 3
atau langsung gunakan hal khusus
CONTOH LIMIT FUNGSI TRIGONOMETRI
1. l i m sin 2x = 0 (*)
x ® 0 tg 3x 0
sin 2x = 3x 2 = 1 . 1 . 2 = 2
2x tg 3x 3 3 3
2. l i m 1 - cos 2x = 0
x ® 0 sin 2x 0
1 - (1 - 2 sin² 2x) = 2 sin² x = sin x = tg x = 0
2 sin x cos x 2 sin x cos cos x
3. l i m 1 - cos x = 0
x ® 0 3x² 0
2 sin² (½x) = sin (½x) . sin (½x) = 1 . 1 . 1 = 1
3 . 4 . (½x) 6 (½x) (½x) 6 6
atau langsung gunakan hal khusus ® Differensial
4. l i m sin x - sin a = 0 (*)
x ® 0 x - a 0
2 cos ½(x+a) sin ½(x-a) = cos ½(x+a) . sin ½(x-a) =
x - a ½ (x - a )
cos ½(x+a) . 1 = cos ½(a+a) . 1 = cos a
atau langsung gunakan hal khusus ® Differensial
MATEMATIKA {BARISAN & DERET GEOMETRI}
- BARISAN GEOMETRI
U1, U2, U3, ......., Un-1, Un disebut barisan geometri, jika
U1/U2 = U3/U2 = .... = Un / Un-1 = konstanta
Konstanta ini disebut pembanding / rasio (r)
Rasio r = Un / Un-1
Suku ke-n barisan geometri
a, ar, ar² , .......arn-1
U1, U2, U3,......,Un
Suku ke n Un = arn-1 ® fungsi eksponen (dalam n)
- DERET GEOMETRI
a + ar² + ....... + arn-1 disebut deret geometri
a = suku awal
r = rasio
n = banyak suku
Jumlah n suku
Sn = a(rn-1)/r-1 , jika r>1
= a(1-rn)/1-r , jika r<1 ® Fungsi eksponen (dalam n)
Keterangan:- Rasio antara dua suku yang berurutan adalah tetap
- Barisan geometri akan naik, jika untuk setiap n berlaku
Un > Un-1 - Barisan geometri akan turun, jika untuk setiap n berlaku
Un < Un-1
Bergantian naik turun, jika r < 0
- Berlaku hubungan Un = Sn - Sn-1
- Jika banyaknya suku ganjil, maka suku tengah
_______ __________
Ut = Ö U1xUn = Ö U2 X Un-1 dst.
- Jika tiga bilangan membentuk suatu barisan geometri, maka untuk memudahkan perhitungan, misalkan bilangan-bilangan itu adalah a/r, a, ar
- Rasio antara dua suku yang berurutan adalah tetap
- DERET GEOMETRI TAK BERHINGGA
Deret Geometri tak berhingga adalah penjumlahan dari
U1 + U2 + U3 + ..............................
¥
å Un = a + ar + ar² .........................
n=1
dimana n ® ¥ dan -1 < r < 1 sehingga rn ® 0
Dengan menggunakan rumus jumlah deret geometri didapat :
Jumlah tak berhingga S¥ = a/(1-r)
Deret geometri tak berhingga akan konvergen (mempunyai jumlah) untuk -1 < r < 1
Catatan:
a + ar + ar2 + ar3 + ar4 + .................
Jumlah suku-suku pada kedudukan ganjil
a+ar2 +ar4+ ....... Sganjil = a / (1-r²)
Jumlah suku-suku pada kedudukan genap
a + ar3 + ar5 + ...... Sgenap = ar / 1 -r²
Didapat hubungan : Sgenap / Sganjil = r
PENGGUNAAN
Perhitungan BUNGA TUNGGAL (Bunga dihitung berdasarkan modal awal)
M0, M1, M2, ............., Mn
M1 = M0 + P/100 (1) M0 = {1+P/100(1)}M0
M2 = M0 + P/100 (2) M0 = {1+P/100(2)} M0
.
.
.
.
Mn =M0 + P/100 (n) M0 ® Mn = {1 + P/100 (n) } M0
Perhitungan BUNGA MAJEMUK (Bunga dihitung berdasarkan modal terakhir)
M0, M1, M2, .........., Mn
M1 = M0 + P/100 . M0 = (1 + P/100) M0
M2 = (1+P/100) M0 + P/100 (1 + P/100) M0 = (1 + P/100)(1+P/100)M0
= (1 + P/100)² M0
.
.
.
Mn = {1 + P/100}n M0
Keterangan :
M0 = Modal awal
Mn = Modal setelah n periode
p = Persen per periode atau suku bunga
n = Banyaknya periode
Catatan:
Rumus bunga majemuk dapat juga dipakai untuk masalah pertumbuhan tanaman, perkembangan bakteri (p > 0) dan juga untuk masalah penyusutan mesin, peluruhan bahan radio aktif (p < 0).
About Me
Labels
- berita unik (1)
- biologi (16)
- fisika (19)
- kata cinta (1)
- kimia (17)
- Matematika (24)


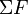 adalah resultan
adalah resultan