Dalam
trigonometri,
hukum sinus ialah pernyataan tentang
segitiga yang berubah-ubah di udara. Jika sisi segitiga ialah (kasus sederhana)
a,
b dan
c dan
sudut yang berhadapan bersisi (huruf besar)
A,
B and
C, hukum
sinus menyatakan

Rumus ini berguna menghitung sisi yang tersisa dari segitiga jika 2 sudut dan 1 sisinya diketahui, masalah umum dalam teknik
triangulasi. Dapat juga digunakan saat 2 sisi dan 1 dari sudut yang tak dilampirkan diketahui; dalam kasus ini, rumus ini dapat memberikan 2 nilai penting untuk sudut yang dilampirkan. Saat ini terjadi, sering hanya 1 hasil akan menyebabkan seluruh sudut kurang daripada 180°; dalam kasus lain, ada 2 penyelesaian valid pada segitiga.
Timbal balik bilangan yang yang digambarkan dengan hukum sinus (yakni
a/sin(
A)) sama dengan
diameter d . Kemudian hukum ini dapat dituliskan
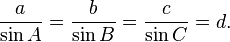
Dapat ditunjukkan bahwa:

di mana
- s merupakan semi-perimeter
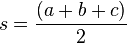
Turunan
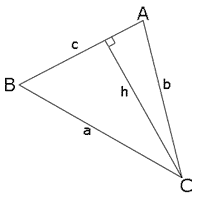
Buatlah segitiga dengan sisi
a,
b, dan
c, dan sudut yang berlawanan
A,
B, dan
C. Buatlah garis dari sudut
C pada sisi lawannya
c yang menonjol sekali dalam 2 segitiga siku-siku, dan sebut panjang garis ini
h.
Dapat diamati bahwa:
 and
and 
Kemudian:

dan
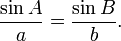
Melakukan hal yang sama dengan garis yang digambarkan antara sudut
A dan sisi
a akan menghasilkan:
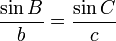

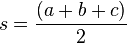
 and
and 


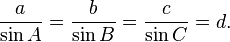

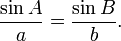

0 comments:
Posting Komentar